⇐ Previous topic|Next topic ⇒
Table of Contents
Chi-square test of independence
Summary
Use the chi-square test of independence when you have two nominal variables and you want to see whether the proportions of one variable are different for different values of the other variable. Use it when the sample size is large.
When to use it
Use the chi-square test of independence when you have two nominal variables, each with two or more possible values. You want to know whether the proportions for one variable are different among values of the other variable. For example, Jackson et al. (2013) wanted to know whether it is better to give the diphtheria, tetanus and pertussis (DTaP) vaccine in either the thigh or the arm, so they collected data on severe reactions to this vaccine in children aged 3 to 6 years old. One nominal variable is severe reaction vs. no severe reaction; the other nominal variable is thigh vs. arm.
| No severe reaction | Severe reaction | Percent severe reaction |
|
|---|---|---|---|
| Thigh | 4758 | 30 | 0.63% |
| Arm | 8840 | 76 | 0.85% |
There is a higher proportion of severe reactions in children vaccinated in the arm; a chi-square of independence will tell you whether a difference this big is likely to have occurred by chance.
A data set like this is often called an "R×C table," where R is the number of rows and C is the number of columns. This is a 2×2 table. If the results were divided into "no reaction", "swelling," and "pain", it would have been a 2×3 table, or a 3×2 table; it doesn't matter which variable is the columns and which is the rows.
It is also possible to do a chi-square test of independence with more than two nominal variables. For example, Jackson et al. (2013) also had data for children under 3, so you could do an analysis of old vs. young, thigh vs. arm, and reaction vs. no reaction, all analyzed together. That experimental design doesn't occur very often in experimental biology and is rather complicated to analyze and interpret, so I don't cover it in this handbook (except for the special case of repeated 2x2 tables, analyzed with the Cochran-Mantel-Haenszel test).
Fisher's exact test is more accurate than the chi-square test of independence when the expected numbers are small, so I only recommend the chi-square test if your total sample size is greater than 1000. See the web page on small sample sizes for further discussion of what it means to be "small".
The chi-square test of independence is an alternative to the G–test of independence, and they will give approximately the same results. Most of the information on this page is identical to that on the G–test page. You should read the section on "Chi-square vs. G–test", pick either chi-square or G–test, then stick with that choice for the rest of your life.
Null hypothesis
The null hypothesis is that the relative proportions of one variable are independent of the second variable; in other words, the proportions at one variable are the same for different values of the second variable. In the vaccination example, the null hypothesis is that the proportion of children given thigh injections who have severe reactions is equal to the proportion of children given arm injections who have severe reactions.
How the test works
The math of the chi-square test of independence is the same as for the chi-square test of goodness-of-fit, only the method of calculating the expected frequencies is different. For the goodness-of-fit test, you use a theoretical relationship to calculate the expected frequencies. For the test of independence, you use the observed frequencies to calculate the expected. For the vaccination example, there are 4758+8840+30+76=13704 total children, and 30+76=106 of them had reactions. The null hypothesis is therefore that 106/13704=0.7735% of the children given injections in the thigh would have reactions, and 0.7735% of children given injections in the arm would also have reactions. There are 4758+30=4788 children given injections in the thigh, so you expect 0.007735×4788=37.0 of the thigh children to have reactions, if the null hypothesis is true. You could do the same kind of calculation for each of the cells in this 2×2 table of numbers.
Once you have each of the four expected numbers, you could compare them to the observed numbers using the chi-square test, just like you did for the chi-square test of goodness-of-fit. The result is chi-square=2.04.
To get the P value, you also need the number of degrees of freedom. The degrees of freedom in a test of independence are equal to (number of rows)−1 × (number of columns)−1. Thus for a 2×2 table, there are (2−1)×(2−1)=1 degree of freedom; for a 4×3 table, there are (4−1)×(3−1)=6 degrees of freedom. For chi-square=2.04 with 1 degree of freedom, the P value is 0.15, which is not significant; you cannot conclude that 3-to-6-year-old children given DTaP vaccinations in the thigh have fewer reactions that those given injections in the arm. (Note that I'm just using the 3-to-6 year olds as an example; Jackson et al. [2013] also analyzed a much larger number of children less than 3 and found significantly fewer reactions in children given DTaP in the thigh.)
While in principle, the chi-square test of independence is the same as the test of goodness-of-fit, in practice, the calculations for the chi-square test of independence use shortcuts that don't require calculating the expected frequencies.
Post-hoc tests
When the chi-square test of a table larger than 2×2 is significant (and sometimes when it isn't), it is desirable to investigate the data further. MacDonald and Gardner (2000) use simulated data to test several post-hoc tests for a test of independence, and they found that pairwise comparisons with Bonferroni corrections of the P values work well. To illustrate this method, here is a study (Klein et al. 2011) of men who were randomly assigned to take selenium, vitamin E, both selenium and vitamin E, or placebo, and then followed up to see whether they developed prostate cancer:
| No cancer | Prostate cancer | Percent cancer |
|
|---|---|---|---|
| Selenium | 8177 | 575 | 6.6% |
| Vitamin E | 8117 | 620 | 7.1% |
| Selenium and E | 8147 | 555 | 6.4% |
| Placebo | 8167 | 529 | 6.1% |
The overall 4×2 table has a chi-square value of 7.78 with 3 degrees of freedom, giving a P value of 0.051. This is not quite significant (by a tiny bit), but it's worthwhile to follow up to see if there's anything interesting. There are six possible pairwise comparisons, so you can do a 2×2 chi-square test for each one and get the following P values:
| P value | |
|---|---|
| Selenium vs. vitamin E | 0.17 |
| Selenium vs. both | 0.61 |
| Selenium vs. placebo | 0.19 |
| Vitamin E vs. both | 0.06 |
| Vitamin E vs. placebo | 0.007 |
| Both vs. placebo | 0.42 |
Because there are six comparisons, the Bonferroni-adjusted P value needed for significance is 0.05/6, or 0.008. The P value for vitamin E vs. the placebo is less than 0.008, so you can say that there were significantly more cases of prostate cancer in men taking vitamin E than men taking the placebo.
For this example, I tested all six possible pairwise comparisons. Klein et al. (2011) decided before doing the study that they would only look at five pairwise comparisons (all except selenium vs. vitamin E), so their Bonferroni-adjusted P value would have been 0.05/5, or 0.01. If they had decided ahead of time to just compare each of the three treatments vs. the placebo, their Bonferroni-adjusted P value would have been 0.05/3, or 0.017. The important thing is to decide before looking at the results how many comparisons to do, then adjust the P value accordingly. If you don't decide ahead of time to limit yourself to particular pairwise comparisons, you need to adjust for the number of all possible pairs.
Another kind of post-hoc comparison involves testing each value of one nominal variable vs. the sum of all others. The same principle applies: get the P value for each comparison, then apply the Bonferroni correction. For example, Latta et al. (2012) collected birds in remnant riparian habitat (areas along rivers in California with mostly native vegetation) and restored riparian habitat (once degraded areas that have had native vegetation re-established). They observed the following numbers (lumping together the less common bird species as "Uncommon"):
| Remnant | Restored | |
|---|---|---|
| Ruby-crowned kinglet | 677 | 198 |
| White-crowned sparrow | 408 | 260 |
| Lincoln's sparrow | 270 | 187 |
| Golden-crowned sparrow | 300 | 89 |
| Bushtit | 198 | 91 |
| Song Sparrow | 150 | 50 |
| Spotted towhee | 137 | 32 |
| Bewick's wren | 106 | 48 |
| Hermit thrush | 119 | 24 |
| Dark-eyed junco | 34 | 39 |
| Lesser goldfinch | 57 | 15 |
| Uncommon | 457 | 125 |
The overall table yields a chi-square value of 149.8 with 11 degrees of freedom, which is highly significant (P=2×10−26). That tells us there's a difference in the species composition between the remnant and restored habitat, but it would be interesting to see which species are a significantly higher proportion of the total in each habitat. To do that, do a 2×2 table for each species vs. all others, like this:
| Remnant | Restored | |
|---|---|---|
| Ruby-crowned kinglet | 677 | 198 |
| All others | 2236 | 960 |
This gives the following P values:
| P value | |
|---|---|
| Ruby-crowned kinglet | 0.000017 |
| White-crowned sparrow | 5.2×10−11 |
| Lincoln's sparrow | 3.5×10−10 |
| Golden-crowned sparrow | 0.011 |
| Bushtit | 0.23 |
| Song Sparrow | 0.27 |
| Spotted towhee | 0.0051 |
| Bewick's wren | 0.44 |
| Hermit thrush | 0.0017 |
| Dark-eyed junco | 1.8×10−6 |
| Lesser goldfinch | 0.15 |
| Uncommon | 0.00006 |
Because there are 12 comparisons, applying the Bonferroni correction means that a P value has to be less than 0.05/12=0.0042 to be significant at the P<0.05 level, so six of the 12 species show a significant difference between the habitats.
When there are more than two rows and more than two columns, you may want to do all possible pairwise comparisons of rows and all possible pairwise comparisons of columns; in that case, simply use the total number of pairwise comparisons in your Bonferroni correction of the P value. There are also several techniques that test whether a particular cell in an R×C table deviates significantly from expected; see MacDonald and Gardner (2000) for details.
Assumptions
The chi-square test of independence, like other tests of independence, assumes that the individual observations are independent.
Examples
Bambach et al. (2013) analyzed data on all bicycle accidents involving collisions with motor vehicles in New South Wales, Australia during 2001-2009. Their very extensive multi-variable analysis includes the following numbers, which I picked out both to use as an example of a 2×2 table and to convince you to wear your bicycle helmet:
| Head injury | Other injury | Percent head injury |
|
|---|---|---|---|
| Wearing helmet | 372 | 4715 | 7.3% |
| No helmet | 267 | 1391 | 16.1% |
The results are chi-square=112.7, 1 degree of freedom, P=3×10−26, meaning that bicyclists who were not wearing a helmet have a higher proportion of head injuries.
Gardemann et al. (1998) surveyed genotypes at an insertion/deletion polymorphism of the apolipoprotein B signal peptide in 2259 men. The nominal variables are genotype (ins/ins, ins/del, del/del) and coronary artery disease (with or without disease). The data are:
| No disease | Coronary artery disease | Percent disease |
|
|---|---|---|---|
| ins/ins | 268 | 807 | 24.9% |
| ins/del | 199 | 759 | 20.8% |
| del/del | 42 | 184 | 18.6% |
The biological null hypothesis is that the apolipoprotein polymorphism doesn't affect the likelihood of getting coronary artery disease. The statistical null hypothesis is that the proportions of men with coronary artery disease are the same for each of the three genotypes.
The result is chi-square=7.26, 2 d.f., P=0.027. This indicates that you can reject the null hypothesis; the three genotypes have significantly different proportions of men with coronary artery disease.
Graphing the results
You should usually display the data used in a test of independence with a bar graph, with the values of one variable on the X-axis and the proportions of the other variable on the Y-axis. If the variable on the Y-axis only has two values, you only need to plot one of them. In the example below, there would be no point in plotting both the percentage of men with prostate cancer and the percentage without prostate cancer; once you know what percentage have cancer, you can figure out how many didn't have cancer.
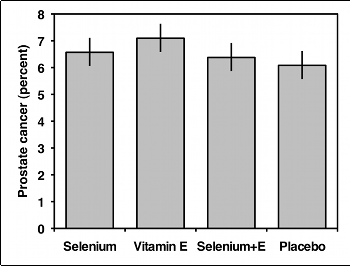
If the variable on the Y-axis has more than two values, you should plot all of them. Some people use pie charts for this, as illustrated by the data on bird landing sites from the Fisher's exact test page:
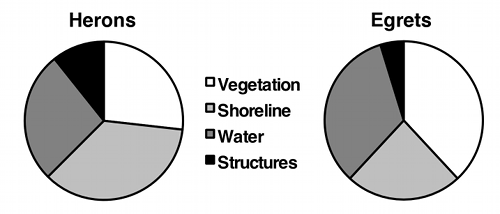
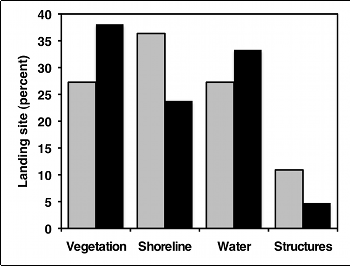
But as much as I like pie, I think pie charts make it difficult to see small differences in the proportions, and difficult to show confidence intervals. In this situation, I prefer bar graphs:
Similar tests
There are several tests that use chi-square statistics. The one described here is formally known as Pearson's chi-square. It is by far the most common chi-square test, so it is usually just called the chi-square test.
The chi-square test may be used both as a test of goodness-of-fit (comparing frequencies of one nominal variable to theoretical expectations) and as a test of independence (comparing frequencies of one nominal variable for different values of a second nominal variable). The underlying arithmetic of the test is the same; the only difference is the way you calculate the expected values. However, you use goodness-of-fit tests and tests of independence for quite different experimental designs and they test different null hypotheses, so I treat the chi-square test of goodness-of-fit and the chi-square test of independence as two distinct statistical tests.
If the expected numbers in some classes are small, the chi-square test will give inaccurate results. In that case, you should use Fisher's exact test. I recommend using the chi-square test only when the total sample size is greater than 1000, and using Fisher's exact test for everything smaller than that. See the web page on small sample sizes for further discussion.
If the samples are not independent, but instead are before-and-after observations on the same individuals, you should use McNemar's test.
Chi-square vs. G–test
The chi-square test gives approximately the same results as the G–test. Unlike the chi-square test, G-values are additive, which means they can be used for more elaborate statistical designs. G–tests are a subclass of likelihood ratio tests, a general category of tests that have many uses for testing the fit of data to mathematical models; the more elaborate versions of likelihood ratio tests don't have equivalent tests using the Pearson chi-square statistic. The G–test is therefore preferred by many, even for simpler designs. On the other hand, the chi-square test is more familiar to more people, and it's always a good idea to use statistics that your readers are familiar with when possible. You may want to look at the literature in your field and see which is more commonly used.
How to do the test
Spreadsheet
I have set up a spreadsheet that performs this test for up to 10 columns and 50 rows. It is largely self-explanatory; you just enter you observed numbers, and the spreadsheet calculates the chi-squared test statistic, the degrees of freedom, and the P value.
Web page
There are many web pages that do chi-squared tests of independence, but most are limited to fairly small numbers of rows and columns. Here is a page that will do up to a 10×10 table.
R
Salvatore Mangiafico's R Companion has a sample R program for the chi-square test of independence.
SAS
Here is a SAS program that uses PROC FREQ for a chi-square test. It uses the apolipoprotein B data from above.
DATA cad; INPUT genotype $ health $ count; DATALINES; ins-ins no_disease 268 ins-ins disease 807 ins-del no_disease 199 ins-del disease 759 del-del no_disease 42 del-del disease 184 ; PROC FREQ DATA=cad; WEIGHT count / ZEROS; TABLES genotype*health / CHISQ; RUN;
The output includes the following:
Statistics for Table of genotype by health
Statistic DF Value Prob
------------------------------------------------------
Chi-Square 2 7.2594 0.0265
Likelihood Ratio Chi-Square 2 7.3008 0.0260
Mantel-Haenszel Chi-Square 1 7.0231 0.0080
Phi Coefficient 0.0567
Contingency Coefficient 0.0566
Cramer's V 0.0567
The "Chi-Square" on the first line is the P value for the chi-square test; in this case, chi-square=7.2594, 2 d.f., P=0.0265.
Power analysis
If each nominal variable has just two values (a 2×2 table), use the power analysis for Fisher's exact test. It will work even if the sample size you end up needing is too big for a Fisher's exact test.
For a test with more than 2 rows or columns, use G*Power to calculate the sample size needed for a test of independence. Under Test Family, choose chi-square tests, and under Statistical Test, choose Goodness-of-Fit Tests: Contingency Tables. Under Type of Power Analysis, choose A Priori: Compute Required Sample Size.
You next need to calculate the effect size parameter w. You can do this in G*Power if you have just two columns; if you have more than two columns, use the chi-square spreadsheet. In either case, enter made-up proportions that look like what you hope to detect. This made-up data should have proportions equal to what you expect to see, and the difference in proportions between different categories should be the minimum size that you hope to see. G*Power or the spreadsheet will give you the value of w, which you enter into the Effect Size w box in G*Power.
Finally, enter your alpha (usually 0.05), your power (often 0.8 or 0.9), and your degrees of freedom (for a test with R rows and C columns, remember that degrees of freedom is (R−1)×(C−1)), then hit Calculate. This analysis assumes that your total sample will be divided equally among the groups; if it isn't, you'll need a larger sample size than the one you estimate.
As an example, let's say you're looking for a relationship between bladder cancer and genotypes at a polymorphism in the catechol-O-methyltransferase gene in humans. In the population you're studying, you know that the genotype frequencies in people without bladder cancer are 0.36 GG, 0.48 GA, and 0.16 AA; you want to know how many people with bladder cancer you'll have to genotype to get a significant result if they have 6% more AA genotypes. Enter 0.36, 0.48, and 0.16 in the first column of the spreadsheet, and 0.33, 0.45, and 0.22 in the second column; the effect size (w) is 0.10838. Enter this in the G*Power page, enter 0.05 for alpha, 0.80 for power, and 2 for degrees of freedom. The result is a total sample size of 821, so you'll need 411 people with bladder cancer and 411 people without bladder cancer.
References
Bambach, M.R., R.J. Mitchell, R.H. Grzebieta, and J. Olivier. 2013. The effectiveness of helmets in bicycle collisions with motor vehicles: A case–control study. Accident Analysis and Prevention 53: 78-88.
Gardemann, A., D. Ohly, M. Fink, N. Katz, H. Tillmanns, F.W. Hehrlein, and W. Haberbosch. 1998. Association of the insertion/deletion gene polymorphism of the apolipoprotein B signal peptide with myocardial infarction. Atherosclerosis 141: 167-175.
Jackson, L.A., Peterson, D., Nelson, J.C., et al. (13 co-authors). 2013. Vaccination site and risk of local reactions in children one through six years of age. Pediatrics 131: 283-289.
Klein, E.A., I.M. Thompson, C.M. Tangen, et al. (21 co-authors). 2011. Vitamin E and the risk of prostate cancer: the selenium and vitamin E cancer prevention trial (SELECT). Journal of the American Medical Association 306: 1549-1556.
Latta, S.C., C.A. Howell, M.D. Dettling, and R.L. Cormier. 2012. Use of data on avian demographics and site persistence during overwintering to assess quality of restored riparian habitat. Conservation Biology 26: 482-492.
MacDonald, P.L., and Gardner, R.C. 2000. Type I error rate comparisons of post hoc procedures for I×J chi-square tables. Educational and Psychological Measurment 60: 735-754.
⇐ Previous topic|Next topic ⇒
Table of Contents
This page was last revised July 20, 2015. Its address is http://www.biostathandbook.com/chiind.html. It may be cited as:
McDonald, J.H. 2014. Handbook of Biological Statistics (3rd ed.). Sparky House Publishing, Baltimore, Maryland. This web page contains the content of pages 59-67 in the printed version.
©2014 by John H. McDonald. You can probably do what you want with this content; see the permissions page for details.
